题目描述 331. 验证二叉树的前序序列化

序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。

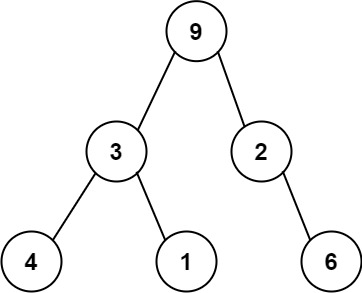
例如，上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#"，其中 # 代表一个空节点。

给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。

保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。

你可以认为输入格式总是有效的

• 例如它永远不会包含两个连续的逗号，比如 "1,,3" 。

注意：不允许重建树。

示例 1:

输入: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
输出: true

示例 2:

输入: preorder = "1,#"
输出: false

示例 3:

输入: preorder = "9,#,#,1"
输出: false

提示:

• 1 <= preorder.length <= 104
• preorder 由以逗号 “，” 分隔的 [0,100] 范围内的整数和 “#” 组成

题解

解法一 栈 + 前序遍历

当遇到两个连续的 “#” ，说明之前的节点是叶子节点，直接将这一部分削减成一个 “#”

class Solution {
    public boolean isValidSerialization(String preorder) {

        String[] preorders = preorder.split(",");
        Deque<String> stack = new ArrayDeque<>();
        for (int i = 0; i < preorders.length; i++) {
            stack.addLast(preorders[i]);
            while (canRemove(stack));
        }
        return stack.size() == 1 && stack.removeLast().equals("#");
    }

    public boolean canRemove(Deque<String> stack) {
        if (stack.size() < 3) return false;
        String temp1 = stack.removeLast();
        String temp2 = stack.removeLast();
        if (temp2.equals("#") && temp1.equals("#") && !stack.peekLast().equals("#")) {
                stack.removeLast();
                stack.addLast("#");
                return true;
        }
        stack.addLast(temp2);
        stack.addLast(temp1);
        return false;
    }
}

解法二 入度和出度

在一个有向图中，入度一定等于出度

• 根节点提供两个出度
• 普通节点提供两个出度，1 个入度
• 叶子节点提供一个入度

class Solution {

    public boolean isValidSerialization(String preorder) {
        String[] preorders = preorder.split(",");
        if (preorders[0].equals("#")) return preorders.length == 1;
        int inCnt = 0, outCnt = 2;
        for (int i = 1; i < preorders.length; i++) {
            inCnt += 1;
            if (!preorders[i].equals("#")) {
                outCnt += 2;
            }
            // 如果某个时刻入度已经等于出度，那这个新加入的元素一定是“#”，在后面不应该有新的子节点
            if (inCnt == outCnt && i != preorders.length - 1) return false;
            if (inCnt > outCnt) return false;
        }
        return inCnt == outCnt;
    }
}