题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

解法

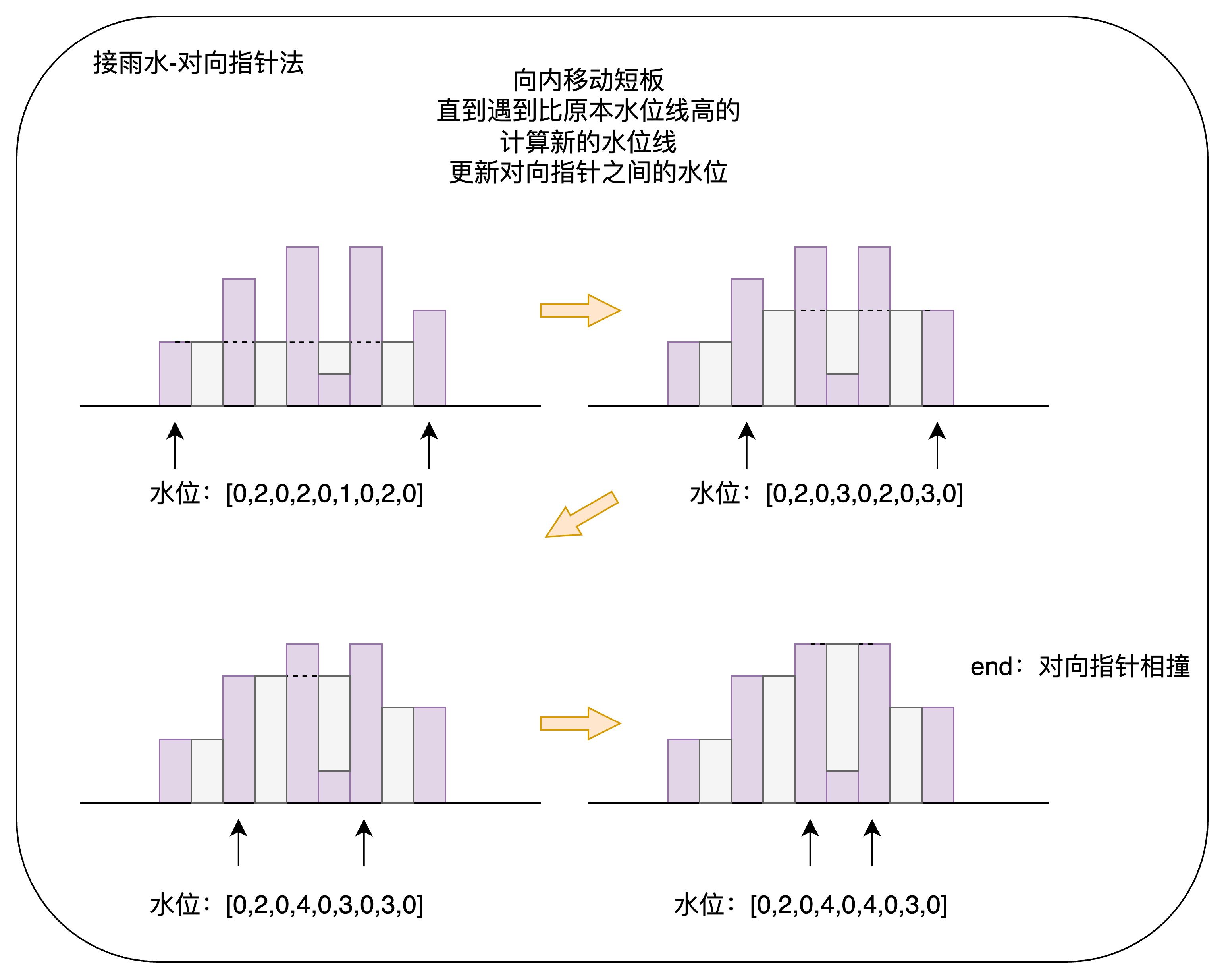
解法一 对向双指针

代码：

class Solution {
    public int trap(int[] height) {
        // 对向双指针
        int left = 0, right = height.length - 1;
        int[] rains = new int[height.length];
        // 短板高度
        int waterLine = 0;
        while (left < right) {
            if (height[left] <= height[right]) {
                if (height[left] > waterLine) {
                    waterLine = height[left];
                    for (int i = left + 1; i < right; i++) 
                        if (height[i] < waterLine) rains[i] = waterLine - height[i];
                }
                left++;
            } else {
                if (height[right] > waterLine) {
                    waterLine = height[right];
                    for (int i = left + 1; i < right; i++) 
                        if (height[i] < waterLine) rains[i] = waterLine - height[i];
                }
                right--;
            }
        }
        int result = 0;
        for (int rain : rains) result += rain;
        return result;
    }
}

首次思路是用对象双指针来做，时间复杂度最差为O(N²) ，虽然一遍过了，但是用时排名很差，看来有优化空间。

优化 – 尝试把for循环优化掉

不需要每次都计算水位，而是将指针处的水位直接设置为水位线的高度。

第一次遍历结束之后，再比较水位线和height。

class Solution {
    public int trap(int[] height) {
        // 对向双指针
        int left = 0, right = height.length - 1;
        // 水位数组
        int[] rains = new int[height.length];
        // 水位线
        int waterLine = 0;
        while (left < right) {
            if (height[left] <= height[right]) {
                if (height[left] > waterLine) 
                    waterLine = height[left];
                rains[left] = waterLine;
                rains[right] = waterLine;
                left++;
            } else {
                if (height[right] > waterLine) 
                    waterLine = height[right];
                rains[left] = waterLine;
                rains[right] = waterLine;
                right--;
            }
        }
        int result = 0;
        for (int i = 0; i < height.length; i++) {
            result += rains[i] > height[i] ? rains[i] - height[i] : 0;
        }
        return result;
    }
}

时间复杂度直接降到了O(N)！

小结

接雨水这道题久闻大名，没想到做起来反而很通顺，解答优化思路很直接。

看解析本题还有其他解法，后续再进行补充。